Asymmetrische Verschlüsselung einfach erklärt:

Vor- und Nachteile asymmetrischer Verschlüsselung mit Beispielen

23.08.2023

Asymmetrische Verschlüsselung ist ein zentraler Baustein moderner IT-Sicherheit. Sie ermöglicht sichere Kommunikation und Datenübertragung, selbst über unsichere Netzwerke. In diesem Beitrag erfahren Sie, wie asymmetrische Verfahren funktionieren, welche Vorteile sie bieten und welche Herausforderungen sie mit sich bringen.

Inhaltsverzeichnis

Was ist Verschlüsselung?
Unterschied Asymmetrische und symmetrische Verschlüsselung
Asymmetrische Kryptografie
Asymmetrische Verfahren
Vor- und Nachteile der asymmetrischen Verschlüsselung
Ausblick

Was ist Verschlüsselung?

Die Verschlüsselung oder auch Kryptografie ist heute aus der IT-Sicherheit nicht mehr wegzudenken, sei es die Verschlüsselung von Dokumenten, E-Mails und Kommunikationswegen oder die Signierung von Daten, um die Echtheit zu gewährleisten. Kryptografie sorgt dafür, dass wir sicher im Netz kommunizieren können, dass wir sicher Daten austauschen können und dass wir sicher Personen, Dienste und Webseiten identifizieren können.

Die Kryptografie befasst sich mit dem Verschlüsseln von Nachrichten und Daten, während die Kryptoanalyse sich mit dem Entschlüsseln und Knacken der kryptografischen Verfahren befasst.

Das Prinzip der Verschlüsselung ist sehr einfach: Ein Klartext (Botschaft, Datei, Dokument, etc.) wird mithilfe eines Schlüssels in einen Geheimtext umgewandelt. Die Art des Schlüssels hängt vom genutzten Verschlüsselungsverfahren ab. Im Laufe der Jahrhunderte und Jahrtausende haben sich viele verschiedene Verfahren entwickelt.

Unterschied Asymmetrische und symmetrische Verschlüsselung

In der digitalen Kryptografie unterscheidet man zwischen symmetrischer und asymmetrischer Verschlüsselung. Bei der symmetrischen Verschlüsselung wird der gleiche Schlüssel für die Ver- und Entschlüsselung benutzt. Der Schlüssel muss also vom Sender verschlüsselter Daten an den Empfänger der Daten übermittelt werden und das möglichst sicher, denn wenn der Schlüssel einem Dritten bekannt wird, kann dieser die verschlüsselten Daten ebenfalls entschlüsseln. Um dieses Problem zu lösen, wurden asymmetrische Verschlüsselungsverfahren entwickelt, die unterschiedliche Schlüssel zum Ver- und Entschlüsseln benutzen.

Asymmetrische Kryptografie

Asymmetrische Verschlüsselungsverfahren bestehen anders als symmetrische Verfahren aus zwei unterschiedlichen Schlüsseln, die durch den Schlüsselalgorithmus mathematisch voneinander abhängig sind: einem öffentlichen (engl. public) und einem privaten (engl. private) Schlüssel. Daher wird es auch oft als Public-Key-Verfahren bezeichnet. Es findet u.a. Einsatz in Public-Key-Infrastrukturen, der Authentifizierung von digitalen Signaturen und bei der Aushandlung von Schlüsseln.

Wie funktioniert asymmetrische Verschlüsselung?

Das Prinzip der asymmetrischen Verschlüsselung ist leicht erklärt: Jeder Kommunikationspartner erzeugt ein eigenes Schlüsselpaar, bestehend aus einem privaten und öffentlichen Schlüssel. Der private Schlüssel muss geheim bleiben, der öffentliche Schlüssel darf weitergegeben werden.

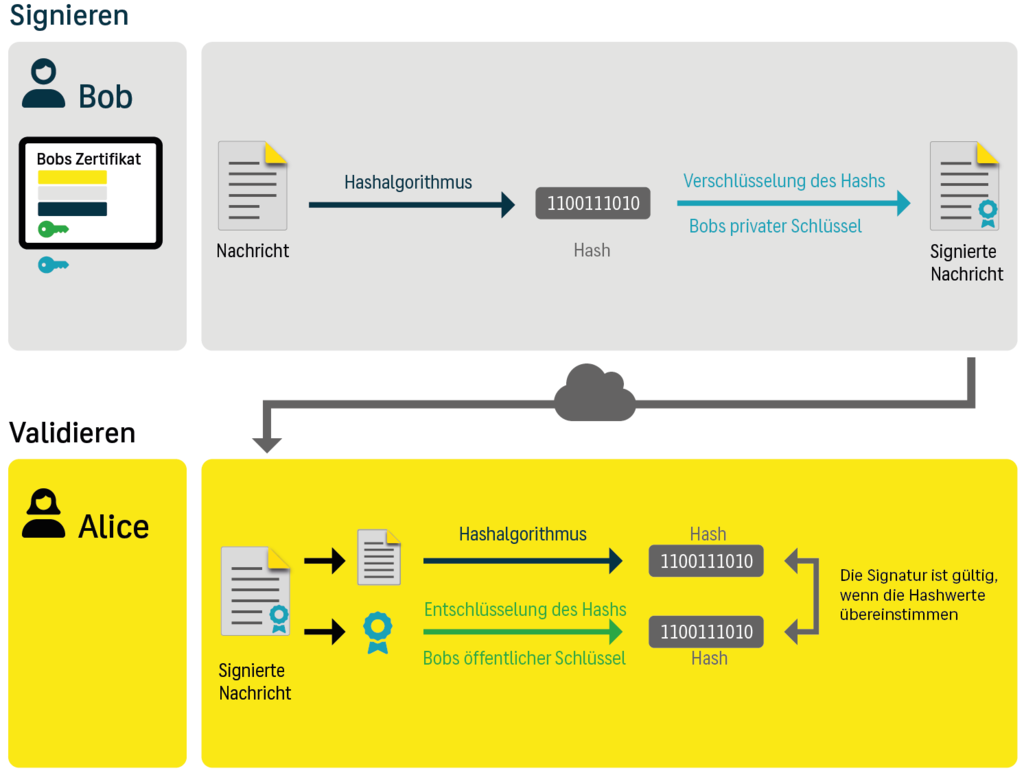
Alice und Bob sind zwei Entitäten, die miteinander kommunizieren wollen. Dabei ist es egal, ob sie tatsächliche Personen oder Geräte, Maschinen, Dienste, etc. sind, denn in der digitalen Welt hat jeder eine eigene Identität. Damit sie sicher kommunizieren können, müssen sie sich sicher sein, dass es sich bei ihrem Gegenüber auch wirklich um Bob oder Alice handelt. Dazu weisen sich die beiden Kommunikationspartner mithilfe von digitalen Signaturen aus. Sie tauschen ihren öffentlichen Schlüssel aus. Bob kann nun mithilfe seines privaten Schüssels etwas signieren. Die signierten Daten schickt er an Alice. Sie kann wiederum mithilfe des öffentlichen Schlüssels von Bob die Signatur prüfen, deren Echtheit feststellen und damit nachweisen, dass Bob in Besitz des zugehörigen privaten Schlüssels ist. Ist sichergestellt das Bob seinen privaten Schlüssel geheim hält, so kann Alice sicher davon ausgehen, dass diese Daten wirklich von Bob stammen.

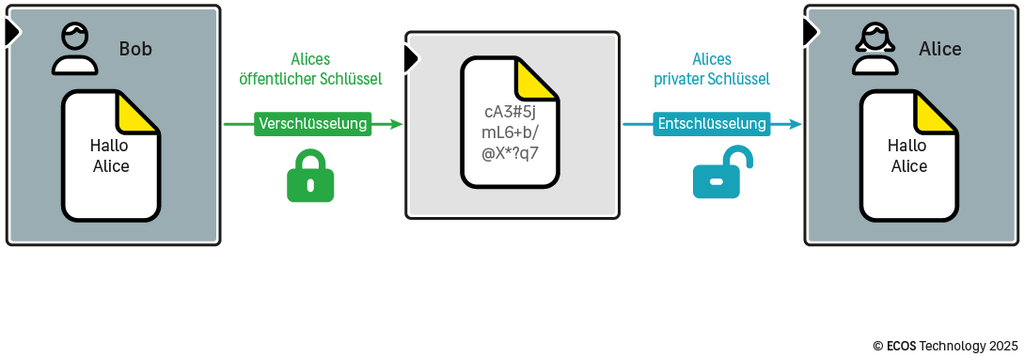
Mit asymmetrischer Kryptografie können aber nicht nur Daten signiert werden, sondern auch Daten verschlüsselt werden. Beide benötigen wiederum den öffentlichen Schlüssel des anderen. In diesem Fall verschlüsselt Bob die Nachricht/Daten mit dem öffentlichen Schlüssel von Alice. Die so entstandenen Daten schickt er an Alice. Sie kann die empfangene Nachricht mit ihrem privaten Schlüssel entschlüsseln und lesen. Dabei spielt es keine Rolle, wie sicher oder unsicher der Kommunikationsweg ist, denn selbst wenn die Nachricht abgefangen werden sollte, kann sie ohne den privaten Schlüssel von Alice nicht entschlüsselt werden.

Mathematische Grundlagen

Zur Berechnung der Schlüsselpaare gibt es verschiedene Schlüsselalgorithmen. Die verschiedenen Algorithmen basieren alle auf sogenannten Falltürfunktionen, einer Sonderform von Einwegfunktionen. Das sind Funktionen, die einfach zu berechnen sind, aber nur sehr aufwendig wieder zurückzurechnen (umzukehren) sind, es sei denn man kennt die Falltür (ein Geheimnis, in diesem Fall den richtigen privaten Schlüssel).

Eine Einwegfunktion muss bestimmte Eigenschaften erfüllen:

Der Funktionswert y ist mit der Funktion y = f(x) und gegebenem x leicht zu berechnen.
Der Funktionswert x ist mit der Umkehrfunktion x = f ^-1(y), wenn y bekannt ist, praktisch nicht zu berechnen.

Einwegfunktionen werden oft mit einem klassischen Telefonbuch aus Papier verglichen: Es ist sehr leicht zu einem Namen die passende Telefonnummer zu finden, weil sie alphabetisch aufgebaut sind, aber umgekehrt wird es sehr schwer zu einer unbekannten Telefonnummer den richtigen Namen zu finden.

Den verschiedenen Verfahren ist gemein, dass die privaten Schlüssel mit aktueller Hardware und Rechenleistung nicht durch Ausprobieren zu erraten sind. Um ein Verfahren zu brechen, wird daher versucht, den Algorithmus zu knacken, damit die Schlüsselsuche soweit eingeschränkt wird, dass die verschlüsselten Daten mit weniger Aufwand und in kürzerer Zeit entschlüsselt werden können.

Asymmetrische Verfahren

Es gibt verschiedene Anwendungsfälle, in denen asymmetrische Kryptografie zum Einsatz kommt:

Schlüsselaustausch
Signieren von Daten
Verschlüsselung

Diffie-Hellman-Schlüsselaustausch

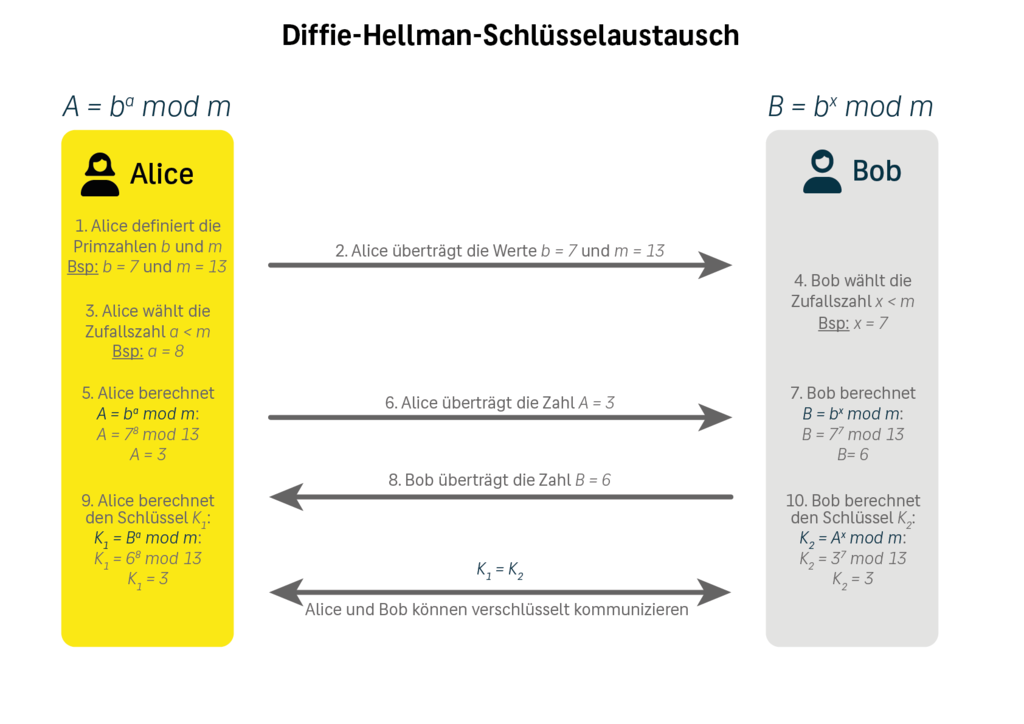
Das Diffie-Hellman-Verfahren löst das Problem des sicheren Schlüsselaustauschs z.B. für eine nachfolgende symmetrische Verschlüsselung, indem nicht der geheime Schlüssel selbst übertragen wird, sondern nur das Ergebnis einer Rechenoperation. Es tauscht also eigentlich nicht den Schlüssel aus, sondern mithilfe des Verfahrens wird ein Schlüssel zwischen zwei Kommunikationspartnern vereinbart.

Das Verfahren nutzt die Einwegfunktion der diskreten Exponentialfunktion und dem diskreten Logarithmus als dazugehörige Umkehrfunktion. Die zugrundeliegende Funktion f(x) = bx mod m ist einfach zu berechnen. Die Umkehrfunktion, um den Exponenten x zu berechnen, ist dagegen so kompliziert, dass die Berechnung bei bester Hardware und mit den besten Algorithmen heute länger als die Lebenszeit unseres Universums dauert, selbst wenn die Werte für b, m und f(x) gegeben sind.

Wollen Alice und Bob jetzt eine sichere Kommunikation aufbauen, tauschen sie im ersten Schritt selbst gewählte Zahlen b und m aus, wobei m eine große Primzahl ist. Alice wählt zusätzlich eine Zufallszahl x. Das Ergebnis der oben erwähnten Funktion sendet sie Bob. Dieser wählt ebenfalls eine eigene Zufallszahl x und sendet das Ergebnis an Alice zurück. Beide berechnen einen Schlüssel mit dem Ergebnis des anderen als b. Das Ergebnis aus dieser Rechenoperation ist gleich und somit haben sie beide den gleichen geheimen Schlüssel.

Ein Angreifer hätte nur die Werte b und m sowie die Ergebnisse der ersten beiden Berechnungen erhalten können, mit denen er den Schlüssel nicht berechnen kann, weil ihm die Zufallszahlen x (der Exponent) von Alice und Bob fehlen, weil diese nicht übertragen werden.

Funktionsweise des Diffie-Hellman-Schlüsselaustauschs — Diffie-Hellman-Schlüsselaustausch

RSA-Verfahren

Das wohl bekannteste und meist verwendete Verfahren ist das RSA-Verschlüsselungsverfahren. Es wurde 1977 von den Mathematikern Ron Rivest, Adi Shamir und Leonard Adleman veröffentlicht. Es kann zur Verschlüsselung und zum digitalen Signieren eingesetzt werden.

Es beruht auf dem Faktorisierungsproblem: Eine zusammengesetzte Zahl (Produkt aus mindestens zwei sehr großen Primzahlen) lässt sich nicht effizient in seine einzelnen Faktoren zerlegen (Primfaktorzerlegung).

Ein einfaches mathematisches Beispiel zeigt, warum das RSA-Verfahren so sicher ist: Gegeben ist das Produkt 48 als Geheimtext der verschlüsselten Daten, dann gibt es zehn mögliche Faktorkombinationen, um das Produkt zu berechnen, wenn nur natürliche Zahlen berücksichtigt werden:

1 x 48 = 48	8 x 6 = 48
2 x 24 = 48	12 x 4 = 48
3 x 16 = 48	16 x 3 = 48
4 x 12 = 48	24 x 2 = 48
6 x 8 = 48	48 x 1 = 48

Sollte nun ein Angreifer den Geheimtext 48 abfangen und weiß, mit welchem Verfahren die Daten verschlüsselt wurden, kennt aber den Schlüssel nicht, dann bleibt ihm nur die Möglichkeit, alle erdenklichen Schlüssel durchzuprobieren.

In diesem Beispiel sind die Möglichkeiten recht überschaubar, aber bei Produkten mit über hundert Stellen wird das schon sehr viel komplizierter. Hinzukommt, dass es durch die Primzahlenzerlegung noch komplizierter wird, weil die Faktoren Primzahlen sein müssen und es daher meist mehr als zwei Faktoren sind, um das Produkt zu berechnen. Für 48 sind es vier Primfaktoren: 48 = 2 x 2 x 2 x 3 (48= 2³ x 3).

Bei einer Schlüssellänge von 256 Bit müssten bei einer vollständigen Schlüsselsuche 10⁷⁶ Schlüssel durchprobiert werden. Im Vergleich dazu ist das Universum nur 10¹⁸ Jahre alt. Aktuell empfiehlt das Bundesamt für Sicherheit in der Informationstechnik (BSI) eine Schlüssellänge von 3072 Bit.

Da die Sicherheit davon abhängt, dass die Umkehrfunktion sehr aufwendig zu berechnen ist, müssen mit steigender Rechenleistung der Hardware, auch die Schlüssellängen für RSA entsprechend länger werden, damit das Verfahren sicher bleibt. Das aktuell sicherste symmetrische Verfahren ist AES (Advanced Encryption Standard) mit Schlüssellängen von 128, 192 oder 256 Bit. Um mit RSA ein gleiches Sicherheitsniveau wie mit AES und einem 128-Bit-Schlüssel zu erhalten, ist ein RSA-Schlüssel mit über 3000 Bit notwendig. Die Sicherheit von AES-256 entspricht einem RSA-Schlüssel von mindestens 15360 Bit. Dadurch ist das Verfahren zwar sehr sicher, aber die Berechnung der Schlüssel würde sehr lange dauern und viel Leistung erfordern, was nicht jede Hardware leisten kann.

ECC-Verfahren

Die Elliptic Curve Cryptography (ECC, deutsch: Elliptische-Kurven-Kryptografie) wurde Mitte der 80er Jahre vorgestellt und gewinnt seit Ende der 90er immer mehr an Bedeutung.

Es handelt sich dabei nicht um ein spezielles Verfahren, sondern um verschiedene Verfahren, die auf elliptischen Kurven basieren, einer Sonderform von algebraischen Kurven. Mithilfe einer Addition, die geometrisch auf diese Kurven definiert ist, wird die Verschlüsselung berechnet. Das Besondere an dem Verfahren ist, dass sich jedes Verfahren, das auf einem diskreten Logarithmus basiert, mit elliptischen Kurven kombinieren lässt, um es zu einem ECC-Verfahren zu machen. Diese werden vor allem für Signaturverfahren und den Schlüsselaustausch eingesetzt.

Durch die Kombination von diskretem Logarithmus auf elliptischen Kurven ist die Notwendigkeit von langen Schlüsseln wie bei RSA nicht gegeben. ECC-Verfahren kommen mit wesentlich kürzeren Schlüsseln aus. Das Sicherheitsniveaus eines AES-256-Schlüssels entspricht dem eines ECC 512-Bit-Schlüssels.

Für die Nutzung eines ECC-Verfahrens müssen die beteiligten Kommunikationspartner dieselbe Kurve verwenden und unterstützen. Da es sehr viele elliptische Kurven gibt, haben u.a. das NIST (National Institute of Standards and Technology) und das BSI (Bundesamt für Sicherheit in der Informationstechnik) Standards für Elliptische Kurven festgelegt.

Bedenken gibt es wegen der Beteiligung der NSA an den NIST-Standards, weshalb Kryptografen empfehlen, eher auf andere Standards auszuweichen.

Die Implementierung von ECC-Verfahren ist sehr fehleranfällig, was die Nutzung von elliptischen Kurven unsicher macht. Ist die Implementierung aber sorgfältig und fehlerfrei verlaufen, bieten ECC-Verfahren eine hohe Sicherheit.

Vor- und Nachteile der asymmetrischen Verschlüsselung

Ein großer Vorteil der asymmetrischen Verschlüsselung ist, dass sie den Schlüsselaustauch über unsichere Netzwerke ermöglicht. Durch die Nutzung von zwei verschiedenen Schlüsseln, wovon einer publik gemacht werden kann, besteht keine Notwendigkeit den geheimen, privaten Schlüssel zum Empfänger zu transportieren.

Ebenso hat jeder Benutzer hat nur zwei Schlüssel, wovon nur einer geheim gehalten werden muss. Bei symmetrischen Verfahren benötigt er für jede Kommunikation und jeden Kommunikationspartner einen anderen Schlüssel, der geheim gehalten werden muss, was auf der einen Seite die Komplexität erhöht und damit auch auf der anderen Seite das Sicherheitsrisiko.

Ein Nachteil ist die erhöhte Rechenleistung von asymmetrischen Verfahren. RSA ist beispielsweise ca. 1000-mal langsamer als AES. Für einen aktuellen Rechner oder Server stellt dies bei kleinen Datenmengen zwar kein Problem dar, aber bei größeren Datenmengen fällt das durchaus ins Gewicht. Kleine Geräte, gerade im IoT-Bereich (Internet of Things) besitzen oftmals nicht genug Rechen- oder Batterieleistung, um asymmetrische Schlüssel berechnen zu können.

Um die Nachteile der asymmetrischen Verfahren zu minimieren, werden sie häufig mit symmetrischen Verfahren kombiniert. Dies wird hybride Verschlüsselung genannt. Die asymmetrische Verschlüsselung wird dann genutzt, um den symmetrischen Schlüssel zu verschlüsseln und sicher zu übertragen. Die eigentlichen Daten werden aber symmetrisch verschlüsselt. Anwendung findet dies z.B. bei der SSL/TLS-Verschlüsselung von Webseiten.

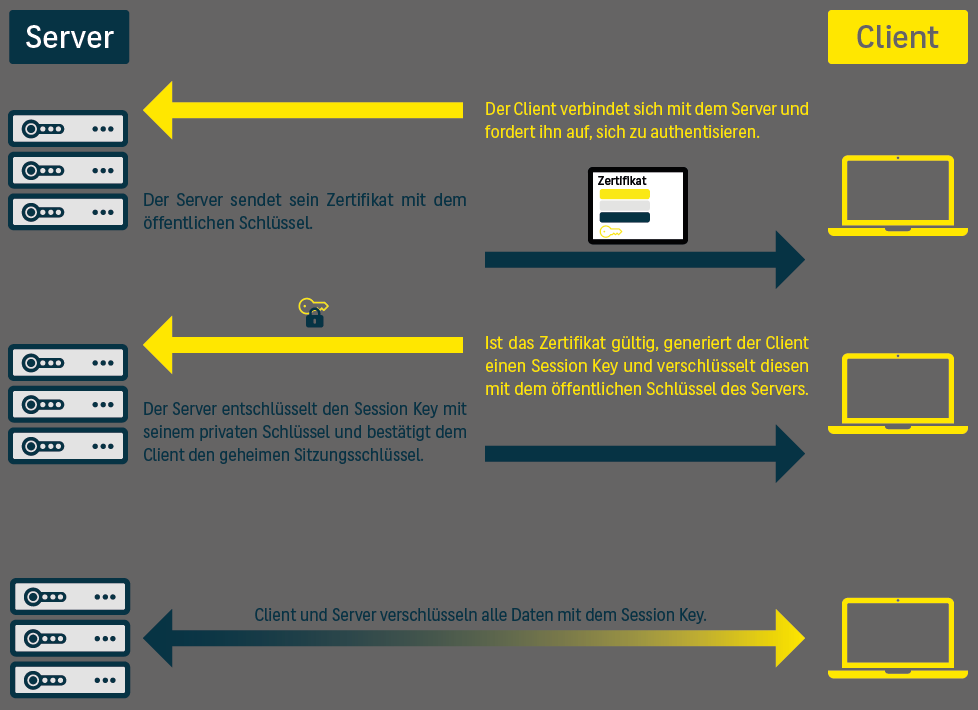
Eine Möglichkeit für einen Verbindungsaufbau bei einer TLS-Verbindung zeigt dies beispielhaft: Ein Client ruft über einen Browser eine Webseite auf, die auf einem externen Webserver gehostet ist. Er bittet den Server, sich zu authentisieren. Der Server schickt sein Zertifikat mit dem öffentlichen Schlüssel an den Client. Dieser prüft das Zertifikat mithilfe des ihm vorliegenden öffentlichen Schlüssels der CA (Informationen zu Zertifikaten und CAs erhalten Sie in unserem PKI-Beitrag). Ist das Zertifikat gültig, generiert der Client einen Session Key (symmetrischer Sitzungsschlüssel), den er mit dem öffentlichen Schlüssel des Servers verschlüsselt. Der Server wiederum kann mit seinem privaten Sitzungsschlüssel den Session Key entschlüsseln, der dann für die Verschlüsselung der Daten und des Datenflusses zwischen Client und Server genutzt wird. Oft kommt hier aber auch das oben beschriebene Diffie-Hellman-Verfahren zum Schlüsselaustausch zum Einsatz.

Ausblick

Die Entwicklung asymmetrischer Verfahren geht immer weiter. Die Schlüssel werden länger oder neue elliptische Kurven werden als Standard implementiert. Doch das wohl größte Problem, was auf die asymmetrische Kryptografie zukommt, sind die Quantencomputer. Asymmetrische Verfahren sind im Gegensatz zu symmetrischen Verfahren nicht quantensicher. Das bedeutet, dass zukünftige Quantencomputer so leistungsstark sind, dass asymmetrische Verfahren mithilfe des Shor-Algorithmus geknackt werden können. Quantencomputer sind bisher nur im Labor möglich, doch es ist nur eine Frage der Zeit, bis sie einer breiteren Masse zugänglich sind. Dann müssen die Algorithmen umgestellt oder ausgetauscht werden. Weitere Informationen dazu erhalten Sie in unserem Whitepaper zu Quantencomputer und Kryptoagilität.

Für mehr Informationen zu den Themen IT-Sicherheit, PKI und unseren Produkten abonnieren Sie unseren Newsletter.